The game of roulette attracts millions of players with the promise of quick and easy profits if only their lucky number would come up on the very next ball toss. The rules of roulette are easy to master but many inexperienced players fail to recognize the common fact that the simpler a given casino game is, the greater the advantage the house holds over those who play it. The same applies in full force to the enticing game of chance that is roulette.
The game may not require players to be mathematical geniuses, yet it would be impossible for them to emerge winners in the long run without gaining a proper understanding of concepts like odds and probabilities. While there is no sure-proof way for a roulette player to make a correct prediction as to which number would hit on the next spin, having at least a basic understanding of odds and probability may help you make better-informed decisions as to which types of bets to place. If you are new to this exciting game of chance, read on for a brief introduction on how the concepts of odds and probabilities apply to roulette.
The Concept of Probability in Roulette
 Before you put your own funds at risk and place your first real-money bets on roulette, you need to get at least a basic understanding of what probability means. Generally speaking, this term is used to denote the likelihood of a given random event occurring. The said likelihood is expressed either in the form of fractions or as a percentage.
Before you put your own funds at risk and place your first real-money bets on roulette, you need to get at least a basic understanding of what probability means. Generally speaking, this term is used to denote the likelihood of a given random event occurring. The said likelihood is expressed either in the form of fractions or as a percentage.
The probability of a random event occurring can be displayed on a line and is assigned a value ranging between 0 and 1 like so 0______1/2______1. At the left side, we have 0 which is to say the random event is impossible and as such, will never take place. Towards the middle of the probability line, the chances of the event occurring are equal or ½. To the right, we have 1 which means the random event is extremely likely to occur.
In roulette, the probability of winning with specific bet types is rather easy to determine. As we know, there are either 37 or 38 possible outcomes per single spin, depending on whether one is playing on a single-zero or a double-zero wheel. Since the results in roulette games are entirely random, there are only two possible outcomes for the players – they either win or lose.
Therefore, the probability of winning with a given bet type is calculated by dividing the number of ways to win by the total number of all possible outcomes. Another way to put it would be to say the probability of winning is equal to the number of ways to win, divided by the total of the ways to win and the ways to lose.
From this, it follows we can calculate the likelihood of winning with a given roulette bet by using the following formula – Probability of winning = Ways to Win / (Ways to Win + Ways to Lose). Let us first demonstrate how it works by using a coin toss as an example.
As you know, when you are flipping a coin, there are only two possible outcomes as the coin will land either on heads, or on tails. The chances of it landing on each of the two sides are practically equal. Using the formula above, we would perform the following calculation: Probability of Heads = 1 / 1 + 1 = 0.50. To convert this result into a percentage, we multiply with by 100 and get 50%.
Now, let us apply the formula from above to calculate the likelihood of collecting a payout with a Split bet in the game of roulette. Since with Split bets players cover only two numbers that are adjacent on the layout, there are only two ways to win out of 37 possible outcomes, i.e. if one is playing on a single-zero European wheel. Another way to put it would be to say there are two ways to win and 35 ways to lose with your Split bet. Therefore, the calculation will go as follows: 2 / (2 + 35) = 0.0540 x 100 = 5.40%. In contrast, the likelihood of winning with the very same bet in American roulette drops down to 5.26%, which coincidentally matches the house edge in double-zero games.
The greater the number of outcomes you cover with a single bet, the higher the probability of winning will be. For instance, let us assume you are interested in experimenting with one of the more exotic roulette bets, like Voisin du Zero, which covers a sequence of seventeen random numbers on the single-zero wheel. The probability of hitting one of these winning numbers is equal to 45.94% or 17 / (17 + 20) x 100 since you are now covering almost half of the entire wheel with one such bet. As you can probably see for yourself, figuring out the probability of winning with different roulette bet types does not require profound mathematical knowledge.
| Type of Bet | Winning Spaces | Payout | Probability |
|---|---|---|---|
| Straight up | Any single number including 0 | 35 to 1 | 2.63% |
| Split | Any two adjoining numbers | 17 to 1 | 5.26% |
| Basket | 0,1,2 or 0,2,3 | 11 to 1 | 7.89% |
| Street | Any three numbers horizontal | 11 to 1 | 7.89% |
| Corner | Any four adjoining numbers | 8 to 1 | 10.53% |
| Six Line | Any six numbers from two rows | 5 to 1 | 15.79% |
| 1st Column | 1,4,7,10,13,16,19,22,25,28,31,34 | 2 to 1 | 31.58% |
| 2nd Column | 2,5,8,11,14,17,20,23,26,29,32,35 | 2 to 1 | 31.58% |
| 3rd Column | 3,6,9,12,15,18,21,24,27,30,33,36 | 2 to 1 | 31.58% |
| 1st Dozen | 1 through 12 | 2 to 1 | 31.58% |
| 2nd Dozen | 13 through 24 | 2 to 1 | 31.58% |
| 3rd Dozen | 25 through 36 | 2 to 1 | 31.58% |
| Odd | 1,3,5,7…33,35 | 1 to 1 | 46.37% |
| Even | 2,4,6,8…34,36 | 1 to 1 | 46.37% |
| Red | Any Red | 1 to 1 | 46.37% |
| Black | Any Black | 1 to 1 | 46.37% |
| 1 to 18 | 1,2,3,4…18 | 1 to 1 | 46.37% |
| 19 to 36 | 19,20,21,22…36 | 1 to 1 | 46.37% |
The Odds of Roulette Bets
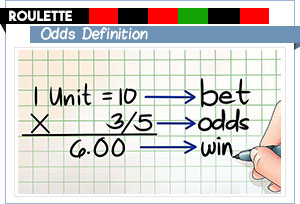 The rules that apply at casino tables are designed in such a way so as to tilt the advantage in favour of the house. Because of this, it is of extreme importance for roulette players to learn how to calculate the odds of winning with each type of bet.
The rules that apply at casino tables are designed in such a way so as to tilt the advantage in favour of the house. Because of this, it is of extreme importance for roulette players to learn how to calculate the odds of winning with each type of bet.
Some people falsely believe the terms “odds” and “probability” can be used interchangeably when in fact, they cannot, simply because they denote two different notions. If you are unfamiliar with the term “odds”, it denotes the ratio between the number of ways to win and the number of ways to lose. Unlike probability, odds are never expressed in terms of percentages but are typically presented as pairs of numbers.
The odds for a random event, like a die toss or a roulette spin, denote the likelihood of this event taking place. To calculate the odds for winning with a given roulette bet, you need to figure out what its probability is. Then you can use the following formula: Odds for Winning = Probability of Winning / (1 – Probability of Winning). If we use the coin flip example from above, the calculation will go as follows: 0.5 / (1 – 0.5) = 1 / 1 which can also be expressed as 1 to 1. The odds in this case are even.
However, there is an easier way to figure out the odds for winning with roulette bets and it is to simply divide the number of ways to win by the number of ways to lose. Therefore, the odds for winning with a Straight Up bet on 32 Red, for example, would be expressed as Odds for Winning = 1/36 or 1 to 36, because there is only one winning number and 36 numbers that result in a loss. As you can see, probability differs from odds in that it is a likelihood of 1 out of 37 outcomes. Similarly, the odds for winning with the Split bet from the earlier example would be 2 to 35 or 2/35.
Some roulette players tend to confuse the odds for winning with the odds against winning because the ratio is written in reverse on many occasions, like so 36 to 1. This is not exactly the same thing because the odds against a given event reflect the probability of the said event not happening. In this case, the formula for calculating the odds against a given bet winning will also be reversed like so: Odds against Winning = Ways to Lose / Ways to Win. Therefore, the odds against winning with a Straight Up bet on 32 Red are equal to 36/1.
These reversed odds are normally used by gambling establishments to list the payouts of the winning bets. The smaller the likelihood of winning with a given roulette bet, the greater the return offered by the house. This is so because when it comes to the majority of casino games, roulette included, the players are practically competing against the house. Therefore, the house is betting against its patrons so the odds paid are the odds against the player winning, hence the inverted ratio. You will be able to read more detailed information regarding the house odds in the section to follow.
| Type of Bet | Winning Spaces | Payout | Odds against Winning |
|---|---|---|---|
| Straight up | Any single number including 0 | 35 to 1 | 36 to 1 |
| Split | Any two adjoining numbers | 17 to 1 | 18 to 1 |
| Basket | 0,1,2 or 0,2,3 | 11 to 1 | 11.33 to 1 |
| Street | Any three numbers horizontal | 11 to 1 | 11.33 to 1 |
| Corner | Any four adjoining numbers | 8 to 1 | 8.25 to 1 |
| Six Line | Any six numbers from two rows | 5 to 1 | 5.167 to 1 |
| 1st Column | 1,4,7,10,13,16,19,22,25,28,31,34 | 2 to 1 | 2.083 to 1 |
| 2nd Column | 2,5,8,11,14,17,20,23,26,29,32,35 | 2 to 1 | 2.083 to 1 |
| 3rd Column | 3,6,9,12,15,18,21,24,27,30,33,36 | 2 to 1 | 2.083 to 1 |
| 1st Dozen | 1 through 12 | 2 to 1 | 2.083 to 1 |
| 2nd Dozen | 13 through 24 | 2 to 1 | 2.083 to 1 |
| 3rd Dozen | 25 through 36 | 2 to 1 | 2.083 to 1 |
| Odd | 1,3,5,7…33,35 | 1 to 1 | 1.056 to 1 |
| Even | 2,4,6,8…34,36 | 1 to 1 | 1.056 to 1 |
| Red | Any Red | 1 to 1 | 1.056 to 1 |
| Black | Any Black | 1 to 1 | 1.056 to 1 |
| 1 to 18 | 1,2,3,4…18 | 1 to 1 | 1.056 to 1 |
| 19 to 36 | 19,20,21,22…36 | 1 to 1 | 1.056 to 1 |
The Casino’s Odds and How they Reflect on Players’ Profitability
 As far as casino games are concerned, there is always a disparity between the mathematical probability of winning with your bets and the ratio these bets are paid at. It is precisely this disparity between the true odds of winning and the casino odds that gives the house advantage over players in the long run.
As far as casino games are concerned, there is always a disparity between the mathematical probability of winning with your bets and the ratio these bets are paid at. It is precisely this disparity between the true odds of winning and the casino odds that gives the house advantage over players in the long run.
For every game the casino offers, the payout odds on bets are established in such a way so that the casino can generate profits on each wager you make. This house advantage is expressed in percentages which reflect the overall return the casino can expect over time, or in other words, the average percentage players will inevitably lose in the long term. Being a commercial business, the casino needs its edge to cover the costs associated with hosting the games. The bottom line is no matter how small this edge is, it can still grind away at one’s bankroll over time.
In some games of chance like craps, there are wild fluctuations in the house edge for different bet types. This is not the case in roulette where the edge remains constant, with a single exception which is the Five-Number bet. The latter can be made in double-zero games only and gives the house an advantage of 7.89%.
To calculate the house edge in roulette, we multiply the difference between the true odds against winning and the casino odds by the probability of winning. On a double-zero wheel, the odds against winning with a Straight Up bet are 37 to 1 but the house pays only 35 to 1 which results in a house edge of 5.26%. As you can see, the difference between the odds against winning and the payout in American roulette is equal to two units. Using the formula from above, we can calculate the house edge like so:
(37/1 – 35/1) x 1/38 = 2/1 x 1/38 = 0.0526 x 100 = 5.26%
The house edge in European roulette is significantly smaller because there is only one zero pocket on the wheel so the calculation will run as follows:
(36/1 – 35/1) x 1/37 = 1/1 x 1/37 = 0.0270 x 100 = 2.70%.
In other words, players will face losses of £27 on average per every £1,000 they bet on European roulette. Please bear in mind that you can expect such losses only over extended periods of time which involve tens of thousands of spins. Everything is possible in the short term, so players can certainly be ahead if they bet on roulette recreationally for a day or two.
Similarly, the odds against winning with a Corner bet (which covers four adjacent numbers on the layout) are 33 to 4 on a single-zero wheel but the casino pays players only 32 to 4 which is to say the house collects a one-unit profit from all winning Corner bets. In American roulette where there are two zeros on the wheel, the casino will profit with two units on such bets because the odds against winning are further increased at 34 to 4 but the payout odds remain 32 to 4.
In games of chance like roulette, there is no escaping the house edge – the more you play, the more you will lose over the long run. That is a why, the roulette variation one plays is of great consequence to their overall, long-term profitability. It makes sense that playing on single-zero wheels is more profitable for players, especially if the La Partage or En Prison Rules are in effect as they decrease the casino advantage to 1.36%.
Calculating the Odds for Consecutive Numbers
 Some players make the mistake to clump two or more successive roulette outcomes together believing that previous winning numbers impact the results on following spins. Such players may witness black coming four times in a row and incorrectly assume the probability of red coming up next is higher because the ball has not landed on a red pocket for a while.
Some players make the mistake to clump two or more successive roulette outcomes together believing that previous winning numbers impact the results on following spins. Such players may witness black coming four times in a row and incorrectly assume the probability of red coming up next is higher because the ball has not landed on a red pocket for a while.
The truth of the matter is this line of thinking is incorrect because the probability of winning with any individual number is always the same, no matter how many times in a row this number has won. It is possible, however, to calculate the combined probability of winning with a given roulette bet two, three or more times in a row. Let us use the Straight Up bet on 9 Red in European roulette as an example to demonstrate how it is done.
The combined probability of winning with 9 Red two consecutive times is the result of the multiplication of the individual probabilities of this number coming up or 1/37 x 1/37 = 1/1369. The likelihood of winning with 9 Red decreases with each subsequent repetition. Therefore, the probability of this individual number appearing three times in a row is equal to 1/37 x 1/37 x 1/37 = 1/50653.
The probability of winning with 9 Red on any given spin is always the same or 1/37. But winning with the same individual number three, four or more times in a row is evidently a rare occurrence. As you can see from the above calculation hitting the same single number three consecutive times amounts to 1 chance in 50,653. This corresponds to a 0.0019% chance of winning with the same number three times in a row.
Note that repeating roulette outcomes by themselves are not that rare phenomena. A number is likely to repeat itself on average once per every 37 tosses of the ball, which is to say 9 Red is likely to hit about two times each hour. It is the number’s consecutive repetition that is a rare event.
Calculating the Odds for Streaks
 Streaks usually occur with even-money bets where the chances of winning and losing are almost equal. Following the same line of reasoning from the previous section, we establish that the likelihood of winning with an even-money bet on Black is equal to 18/37 on a European wheel since there are 18 winning pockets out of 37.
Streaks usually occur with even-money bets where the chances of winning and losing are almost equal. Following the same line of reasoning from the previous section, we establish that the likelihood of winning with an even-money bet on Black is equal to 18/37 on a European wheel since there are 18 winning pockets out of 37.
If Red has hit three consecutive times, the likelihood of Black coming up next remains 18/37. The same is valid for Red hitting on the fourth spin. In fact, this applies to every even-money bet, be it High/Low, Red/Black or Odd/Even, as the probability of each of these outcomes is always 18/37 on a single-zero wheel. Little does it matter what the outcome of the previous spin was.
The likelihood of a winning streak occurring with even-money bets is calculated the same way as that of individual numbers winning several times in a row. In other words, we need to multiply the individual probabilities of the outcome. Thus, the likelihood of experiencing a good streak with Black by winning three consecutive times would be equal to 18/37 x 18/37 x 18/37 = 5832/50653 = 1/8.68. Therefore, such a streak is likely to occur once every eight and a half tosses of the ball on average.
It is also possible to figure out what the likelihood of a losing streak is. Since even-money bets lose whenever the ball falls into the green zero pocket, the probability of losing on Black, for example, is 19/37 on a European wheel because there are 19 ways to lose out of 37 possible outcomes. The formula for a losing streak is the same as that for a winning streak. The likelihood of losing three times in a row with Black is 19/37 x 19/37 x 19/37 = 6859/50653 = 1/7.38. This is to say, you will experience three consecutive losses with even-money bets once per every 7.4 on average.
| Consecutive Hits | Single Zero Probability | Single Zero Odds | Double Zero Probability | Double Zero Odds |
|---|---|---|---|---|
| 1 | 1 in 2.06 | 1.06 to 1 | 1 in 2.11 | 1.11 to 1 |
| 2 | 1 in 4.22 | 3.22 to 1 | 1 in 4.45 | 3.45 to 1 |
| 3 | 1 in 8.68 | 7.68 to 1 | 1 in 9.39 | 8.39 to 1 |
| 4 | 1 in 17.83 | 16.83 to 1 | 1 in 19.82 | 18.82 to 1 |
| 5 | 1 in 36.65 | 35.65 to 1 | 1 in 41.82 | 40.82 to 1 |
| 6 | 1 in 75.31 | 74.32 to 1 | 1 in 88.24 | 87.24 to 1 |
| 7 | 1 in 154.77 | 153.77 to 1 | 1 in 186.20 | 185.20 to 1 |
| 8 | 1 in 318.05 | 317.05 to 1 | 1 in 392.88 | 391.88 to 1 |
| 9 | 1 in 653.59 | 652.59 to 1 | 1 in 828.98 | 827.98 to 1 |
| 10 | 1 in 1343.13 | 1342.13 to 1 | 1 in 1749.14 | 1748.14 to 1 |
- American Roulette
- Best Real-Money Roulette Sites
- Best Roulette Systems
- Double Action Roulette
- Double Ball Roulette
- European Roulette
- French Roulette
- High Roller Roulette
- Most Popular Roulette Games
- Phenomenal Live Roulette (Luckystreak)
- Play Roulette Online
- Progressive Jackpot Roulette
- Roulette Bets and Betting Patterns
- Roulette Rules
- Roulette Strategies
- Roulette Variations
- Ultimate Roulette (Ezugi) Means Extreme Casino Fun













